Nas postagens anteriores, tratamos de introduzir a análise de regressão, e de formaliza-la matematicamente, no presente artigo, iremos introduzir a mais utilizada modelagem de regressão, o modelo de regressão linear simples, também conhecido como modelo de regressão linear simples clássico.
A linearidade nos parâmetros por sua vez aponta para o fato de E(Y|X) ter ou não uma relação linear com os parâmetros beta 1 e beta 2. Os critérios são parecidos, caso os parâmetros tenham índice igual a 1 e não estarem multiplicados ou divididos por qualquer outro parâmetro, então são lineares, caso contrário não o são.
Isso será feito no próximo artigo.
Antes, vamos estudar a essência do termo modelo de regressão linear simples, um modelo de regressão é uma relação matemática entre uma série de variáveis, que parte da estimação de uma relação matemática funcional que explique como a média de uma variável varia em função da média de uma ou mais variáveis independentes. Partindo disso é aparentemente óbvio a essência do termo linear, mas é preciso se aprofundar um pouco mais nesse aspecto. O termo linear, remete a linha, no jargão matemático, remete a uma relação de "reta" entre duas variáveis, em linguagem matemática, isso é dado por:
Sendo y uma variável dependente, x uma variável independente, a o coeficiente linear (o valor que Y assume quando X = 0) e b o coeficiente angular, que representa a inclinação da curva. Essa relação funcional ganha o nome de linear graças a relação dada entre as variáveis, que em um plano cartesiano, é representado por uma reta, para observar melhor, vamos trabalhar com alguns valores matemáticos, suponha a função dada por:
Essa é uma definição matemática-funcional do termo linear, mas em termos econométricos, a linearidade tem dois diferentes sentidos, a linearidade nas variáveis e a linearidade nos parâmetros.
Em termos de econometria, um modelo linear de duas variáveis é dado por:
Como já mostramos anteriormente, o termo E(Y|X) é a média de Y condicionada a uma variável X, o termo linear supõe que a média da variável Y é uma relação linear da variável X com dois parâmetros, assim como na função linear da matemática, onde há um parâmetro de coeficiente linear (beta 1) e um parâmetro de coeficiente angular (beta 2). Conforme veremos, esses parâmetros são a grande incógnita do método econométrico.
Essa é a forma "padrão" de modelo linear, mas não necessariamente somente essa forma funcional ganha o nome de linear. Para entender, vamos compreender os dois aspectos da linearidade:
Essa é a forma "padrão" de modelo linear, mas não necessariamente somente essa forma funcional ganha o nome de linear. Para entender, vamos compreender os dois aspectos da linearidade:
A linearidade nas variáveis diz respeito ao fato da média de Y condicionada X ser linearmente relacionada a variável X ou não.
O critério é a variável X é essencialmente o seguinte, se a derivada de E(Y|X) com relação a X for independente do valor de X, então é uma relação linear, caso contrário, não o é. Em termos mais simples, se X tiver expoente igual a 1 e não estiver multiplicado ou dividido por qualquer instância de X, então dizemos que há uma relação linear.
Para entender, suponha duas formas funcionais dadas por:
Você consegue identificar qual é linear em relação as variáveis? Observe que, para a primeira forma funcional, temos que X tem expoente igual a 1 e não está multiplicado ou dividido por nenhuma instância de X. Em termos de cálculo diferencial:
Já no segundo caso, observe que X não está multiplicado ou dividido por qualquer instância de X, entretanto tem índice igual a 2, o que aponta não linearidade de E(Y|X) em relação a X. Em termos de cálculo diferencial:
Observe que a derivada de E(Y|X) com respeito a X depende do valor de X, o que aponta não linearidade nas variáveis.
A linearidade nos parâmetros por sua vez aponta para o fato de E(Y|X) ter ou não uma relação linear com os parâmetros beta 1 e beta 2. Os critérios são parecidos, caso os parâmetros tenham índice igual a 1 e não estarem multiplicados ou divididos por qualquer outro parâmetro, então são lineares, caso contrário não o são.
Retomando as duas funções anteriores:
A primeira função embora seja linear nas variáveis, não o é nos parâmetros, dado que beta 2 está elevado ao quadrado. Já a segunda função embora não seja linear nas variáveis, é nos parâmetros, dado que beta 1 e beta 2 não estão divididos ou multiplicados entre si, e ambos tem expoente igual a 1.
Agora que se tem em mente os dois conceitos de linearidade, vem a pergunta: qual é o mais relevante? Para fins de econometria, chamaremos de modelo linear os modelos que sejam linear nos parâmetros, sendo ou não linear nas variáveis. Ou seja, ao se deparar com um modelo, você saberá se está lidando com um modelo linear se os parâmetros forem linearmente relacionados a esperança de Y.
Agora que já analisamos o significado de modelo de regressão linear, resta entendermos o termo "simples". Esse termo é utilizado pois somente trabalhamos com duas variáveis, uma dependente e uma independente, caso trabalhemos com duas ou mais variáveis dependentes estaremos de frente com um modelo de regressão múltipla. É importante se atentar a esse aspecto, pois raramente lidaremos com uma análise onde as respostas a variação de apenas uma variável é estudada, embora seja esse o horizonte que iremos estudar por ora. Na vida real, uma variável geralmente é determinada por várias outras variáveis, essa análise de mais de duas variáveis será objeto de estudo futuro, por ora basta analisarmos o modelo de regressão linear simples.
Por fim, podemos então resumir o Modelo de Regressão Linear Simples como o modelo econométrico que permite estudar como a média de uma variável E(Y|X) varia em relação as variações na média de uma variável explicativa X, supondo que essa relação é linear nos parâmetros.
Em termos gerais, podemos definir o MRLS com a seguinte forma funcional:
Entretanto, essa é a forma funcional da FRP, e como dito, trabalharemos com a FRA, uma estimativa para a verdadeira FRP, senda dado por:
Onde o sobrescrito "^" aponta que trata-se de um estimador, ou seja, uma estimativa do valor real, do parâmetro Y como função linear da estimativa dos valores Beta 1 e Beta 2. Trata-se de um ponto essencial, pois o grande objetivo da análise de regressão linear simples é buscar descobrir os verdadeiros valores de beta 1 e beta 2, os dois parâmetros da função linear. Estimando esses parâmetros é possível encontrar a função de regressão amostral que mais se aproxime da função de regressão populacional real. Aprenderemos a estimar esses parâmetros em breve, a partir do método dos mínimos quadrados ordinários (MQO).
Como explicado anteriormente, trata-se de uma especificação determinística, que não leva em conta o elemento estocástico, que representa os erros de previsão, que é dado pelos resíduos: Agora que se tem em mente a essência do Modelo de Regressão Linear Simples é preciso deduzir algumas propriedades e formular algumas hipóteses necessárias para fins de análise.
Mas antes, vale uma reflexão.
Você já parou pra pensar na relevância das relações lineares na ciência econômica? Ao se estudar o modelo de regressão linear, é interessante observar como esse tipo de relação é presente na economia! Para demonstrar, aqui vão alguns exemplos de relações lineares presentes na teoria econômica:
Bibliografia:
GUJARATI, Damodar N; PORTER, Dawn C. Basic Econometrics. 5ª Edição. New York. The McGraw-Hill, 2008.
GUJARATI, Damodar N; PORTER, Dawn C. Basic Econometrics. 5ª Edição. New York. The McGraw-Hill, 2008.










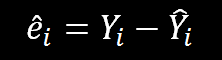


Gostou do conteúdo? Deixe seu comentário! Não gostou? Deixa também, queremos ouvir sua opinião!
ResponderExcluirSiga nossa página no Instagram: @agenteracional