Em um artigo passado, detalhamos a lógica por traz da análise de regressão, o instrumento utilizado pela econometria para analisar a relação entre duas ou mais variáveis. Nesse artigo iremos formalizar o modelo geral de uma análise de regressão. Para começar, será analisado um modelo com apenas duas variáveis, Y e X.
AVISO: Até agora não foi necessário grandes conhecimentos em demais disciplinas, mas para formalizar o modelo de regressão é preciso uma certa carga de conhecimento em inferência e probabilidade, principalmente no que tange a ideia de variável aleatória. Também será exigido conhecimento sobre funções matemáticas.
Até agora definimos a análise de regressão como o estudo de uma variável em função de outras variáveis, mas como isso é justificado probabilisticamente? Temos o análise de regressão como o estudo de como uma variável varie em função da média de outras variáveis. Trocando por miúdos, é analise de qual o valor esperado de Y dado um valor de X, em termos probabilísticos, temos então uma probabilidade condicionada, expressa como:
O que se enxerga a uma primeira vista? Uma clara relação positiva entre as duas variáveis, dado que a medida que a renda se eleva, o consumo se eleva. Isso é uma visão óbvia, mas como analisar isso com o rigor probabilístico? Através de um modelo de regressão. Essa análise de regressão se baseia em analisar como o valor esperado de Y varia em função do valor de X, ou seja, o grande objetivo é estudar qual valor esperado de Y dado o valor fixado de X.
Como interpretar esses resultados? Observe que a medida em que a renda aumenta, a média de despesas de consumo aumenta, isso aponta uma relação positiva, entre as duas variáveis. A grande questão da análise de regressão é criar uma função matemática representativa dessa relação, relembrando o formato funcional que estabelecemos para a regressão:
Essa função é chamada de função de regressão populacional que pode ser definida como a reta que passa por todas as médias condicionadas de Y, para melhor enxergar, vamos plota-la frente ao gráfico de dispersão.
Cada um desses modelos se encaixa melhor conforme os dados são dispersos, por exemplo, no caso vimos uma óbvia tendência linear, o que é razoável supor que a Função de Regressão Populacional assuma um formato linear, mas o mesmo modelo não seria eficiente em um caso de óbvia tendência exponencial, como por exemplo:
Nesse caso não é prudente aplicar um modelo linear para analisar, sendo mais recomendado uma regressão exponencial. Mas ao longo do curso será trabalhado somente a hipótese da linearidade, que é a suposição simples de que a relação entre duas variáveis pode ser expressa em uma reta linear. Isso será melhor desenvolvido no próximo artigo onde será apresentado o modelo de regressão linear simples.
Portanto, o grande objetivo agora se torna encontrar o formato funcional da função de regressão populacional. Descobrindo esse formato funcional podemos estudar a relação e o seu grau.;
Acontece que antes de descobrir como se "achar" a função de regressão populacional é preciso detalhar um ponto sobre a função de regressão populacional.
Como visto em artigo anterior, a análise de regressão não busca (e nem poderia) uma previsão exata, portanto precisamos definir uma modelagem estocástica, afirmando que a função de regressão populacional não é igual aos valores observados, essencialmente:
Para entender o componente estocástico, vamos retomar o exemplo da tabela:
Observe que para X = 80 a Função de Regressão Populacional prevê que a faixa de "consumo" deve ser igual a 65, entretanto, há 4 amostras que divergem desse valor. O erro de cada amostra seria a diferença entre o valor de consumo previsto para cada faixa de renda e a renda específica, se representarmos os erros, nessa tabela, você observará os seguintes erros de previsão:
Reorganizando em tabela as duas amostras:
Observe que cada uma das duas apresentam médias condicionadas diferentes, tal que se plotarmos as duas funções de regressão amostral em um gráfico (não entraremos em detalhes sobre como chegamos nelas nele nesse artigo) obtemos:
Qual das duas é mais precisa? Para saber disso basta enxergar qual a que mais se aproxima da função de regressão populacional, para isso comparamos os valores com o valor obtido pela FRP, visualizando:
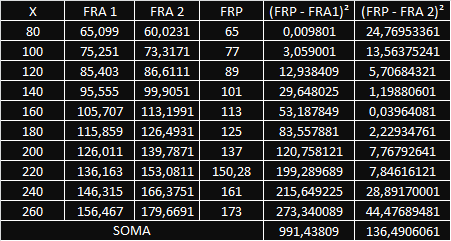
A primeira vista a segunda função de regressão é mais próxima, isso é real? Para confirmar vamos calculara diferença geométrica pela tabela:
Com isso fica claro a influência da amostra escolhida, o objetivo agora torna-se mais óbvio, encontrar a Função de Regressão Populacional escolhendo a melhor (mais próxima) Função de Regressão Amostral.
Como ficará claro, o critério para escolher a função de regressão amostral mais adequada são os erros amostrais, o elemento estocástico.
A ferramenta que será utilizada para chegar a esse resultado é a inferência estatística.
Uma vez compreendido a essência do Modelo de Regressão Simples, no próximo artigo, iremos então desenvolver o principal instrumento de análise de regressão que será utilizada na econometria: O Modelo de Regressão Linear Simples.
Bibliografia:
GUJARATI, Damodar N; PORTER, Dawn C. Basic Econometrics. 5ª Edição. New York. The McGraw-Hill, 2008.

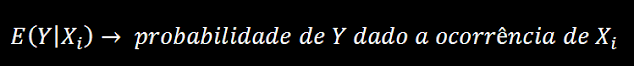





















Gostou do conteúdo? Deixe seu comentário! Não gostou? Deixa também, queremos ouvir sua opinião!
ResponderExcluirSiga nossa página no Instagram: @agenteracional